Este artigo é uma recomendação sobre a representação gráfica de dados biológicos. Estarei utilizando a linguagem de programação R. Orientações de como instalar o R em seu computador e algumas noções básicas em R podem ser encontradas em http://danieltiezzi.pro.br/learn_r/.
Variáveis qualitativas ou categóricas - também denominados de variáveis nominais, de classe ou fatores. os valores são distintos uns aos outros, e cada categoria ou classe são denominadas de níveis. Exemplos de dados categóricos são raça, sexo ou subtipo tumoral. As variáveis categóricas pode ser nominais ou ordinais. Nas ordinais, existem uma ordenação das variáveis, como por exemplo o grau de diferenciação histológica de uma neoplasia (graus 1, 2 e 3);
Variáveis quantitativas - são variáveis que podem ser medidas em uma escala numérica. Elas podem ser contínuas ou discretas. Uma variável contínua pode assumir qualquer número real e pode ser restrita a um intervalo. Exemplos de variável contínua seira peso, altura ou tempo. Já uma variável discreta são aquelas que assume um número contável de valores, um número inteiro. Exemplos são número de filhos ou quantidade de cigarros fumados ao dia.
Antes da análise dos dados é necessários definirmos qual o tipo de dado e compreendermos como é a distribuição das amostras. No caso de variáveis qualitativas, observar a distribuição das amostras é uma tarefa simples. Basta calcular a proporção de cada classe dentro do co conjunto de amostras.
No caso de variáveis quantitativas, nós utilizamos dois parâmetros de análise. O primeiro é chamado de medida de tendência central. Esta medida é importante para termos uma idéia da grandeza da variável. O outro parâmetro é estimar a variabilidade dos valores.
Podemos utilizar três parâmetros para estimar a tendência central de uma variável: média, mediana e moda. Vamos entender como calcular cada um deles e quando aplicar.
Média geralmente utilizamos a média aritmética que é representada pela letra grega µ (mu) ou por \(\bar{x}\). A média aritmética é calculada pela soma de todos os valores dividido pelo número total de amostras:
\(\bar{x}\) = \(\sum_{i=1}^{n} x_i / n\) , onde n é o número de amostras e \(x_i\) é cada um dos valores da variável.
Exemplo de cálculo da média para a idade de 7 indivíduos:
idade = c(34, 23, 37, 55, 87, 47, 41)
média = (34 + 23 + 37 + 55 + 87 + 47 + 41) / 7
média = 46.28
Mediana é o valor central da distribuição dos dados. Para obter a mediana, precisamos ordenar os dados e, o valor que divide a amostra em duas partes iguais é a mediana. Se o número de amostra for par, devemos somar os dois elementos centrais e dividir por dois.
Exemplo de cálculo da mediana para a idade de 7 indivíduos:
idade = c(34, 23, 37, 55, 87, 47, 41)
idade_ordem = (23, 34, 37, 41, 47, 55, 87)
mediana = 41
Moda é o valor mais frequente em um conjunto de dados. A moda não é um valor útil em distribuições contínuas e o conjunto pode ser amodal, se todos os valores têm a mesma frequência.
Existe uma série de medidas de dispersão que podem ser utilizadas para inferir a variabilidade da amostra. As medidas mais utilizadas são a amplitude interquartil e o desvio padrão (variância). Vamos ver seus conceitos e como calcular.
Amplitude interquartil para entendermos este conceito, precisamos definir o conceito de quartil. Vimos que a mediana é o valor que divide o conjunto de dados em dois. Os quartis são os valores que dividem o conjunto de dados em 4, e denominamos esses valores de primeiro (Q1), segundo (Q2) e terceiro (Q3) quartis. A mediana é equivalente ao Q2. Existem diferentes algoritmos para o cálculo dos quartis. Podemos utilizar a seguinte fórmula após ordenar os dados de forma crescente:
Posição do quartil(porcentagem) = porcentagem * (n + 1), onde n = número total de amostras.
A amplitude interquartil é calculada pela diferença entre o Q3 e Q1. Esta medida de dispersão reflete o tamanho da variação onde 50% dos valores centrais do conjunto de amostras se encontram. Vamos ver um exemplo onde temos 20 valores correspondentes a expressão do gene1:
gene1 = c(3.75, -3.40, 3.49, 11.90, 14.41, 7.99, 5.94, 6.15, 10.39, 10.14, 15.36, 5.88, 13.13, 11.60, 7.36, 12.58, 13.85, 14.06, 9.44, 11.42)
Primeiro temos que ordenar os valores de forma crescente:
gene1_order = c(-3.40, 3.49, 3.75, 5.88, 5.94, 6.15, 7.36, 7.99, 9.44, 10.14, 10.39, 11.42, 11.60, 11.90, 12.58, 13.13, 13.85, 14.06, 14.41, 15.36)
Q1 = 0.25 * (20 + 1), então
Q1 = 5.25
Como não temos esta posição, utilizamos a média do valor entre o valor da posição 5 e 6:
Q1 = 5.94 + 6.15, então
Q1 = 6.04
O mesmo se aplica para o Q2 e Q3:
Q2 = 10.26
Q3 = 12.85
A amplitude interquartil (AI) será:
AI = 12.85 - 6.04, então
AI = 6.81
Variância e desvio padrão. A variância é uma medida de dispersão em torno da média e é representada por \(s^2\) ou \(\sigma^2\). A fórmula para o cálculo é baseado na soma dos quadrados do desvio da média:
\(\sigma^2 = \sum_{i=1}^{n} (xi - \bar{x})^2 / (n - 1) = (\sum_{i=1}^{n} xi^2 - (\sum_{i=1}^{n} xi)^2 ) / (n - 1)\)
Note que a variância tem o inconveniente de ter a sua unidade de medida o quadrado da medida da variável. Desta forma, a medida de variação mais utilizada é o desvio padrão \(s\) ou \(\sigma\), que é definido pela raiz quadrada da variância:
\(\sigma = \sqrt{\sum_{i=1}^{n} (xi - \bar{x})^2 / (n - 1)}\)
A análise descritiva pode utilizar tabelas ou gráficos para apresentação dos dados de um casuística. Utilizei o script abaixo para acessar dados sobre gênero, peso, altura e idade de 250 crianças (banco de dados kid.weights). Criei mais uma variável raça de forma aleatória e calculei o índice de massa corporal (BMI, do inglês Body Mass Index).
library(UsingR)
data(kid.weights)
kid.weights$race <- sample(c('white', 'black', 'Hispanic', 'asian'), 250, replace = TRUE, prob = c(0.4, 0.3, 0.25, 0.05))
kid.weights$bmi <- (kid.weights$weight / (kid.weights$height)^2) * 703Temos o peso em libras, a altura em polegada, o IMC em kg/\(m^2\) e idade em meses como variáveis quantitativas contínuas. Como variáveis qualitativas, temos gênero e a raça.
Para as variáveis qualitativas, podemos utilizar o scrip abaixo e descrever a amostra na Tabela 1:
# gênero
table(kid.weights$gender)
round(prop.table(table(kid.weights$gender))*100, 2)
# raça
Tabela 1. Variáveis qualitativas.
| Variável | n | % |
|---|---|---|
| Gênero | ||
Masculino |
121 | 51.6 |
Feminino |
129 | 48.4 |
| Raça | ||
Branco |
99 | 39.6 |
Negro |
70 | 28 |
Hispânico |
71 | 28. 4 |
Asiático |
10 | 4 |
A descrição de dados qualitativos em tabelas é bem aceitável. Podemos usar a tabela para demonstrar como é a distribuição entre duas variáveis qualitativas. Veja a Tabela 3 abaixo:
Tabela 2. Distribuição de gênero e raça.
| Gênero / Raça | Masculino | Feminino |
|---|---|---|
| Branco | 51 | 48 |
| Negro | 30 | 40 |
| Hispânico | 35 | 36 |
| Asiático | 5 | 5 |
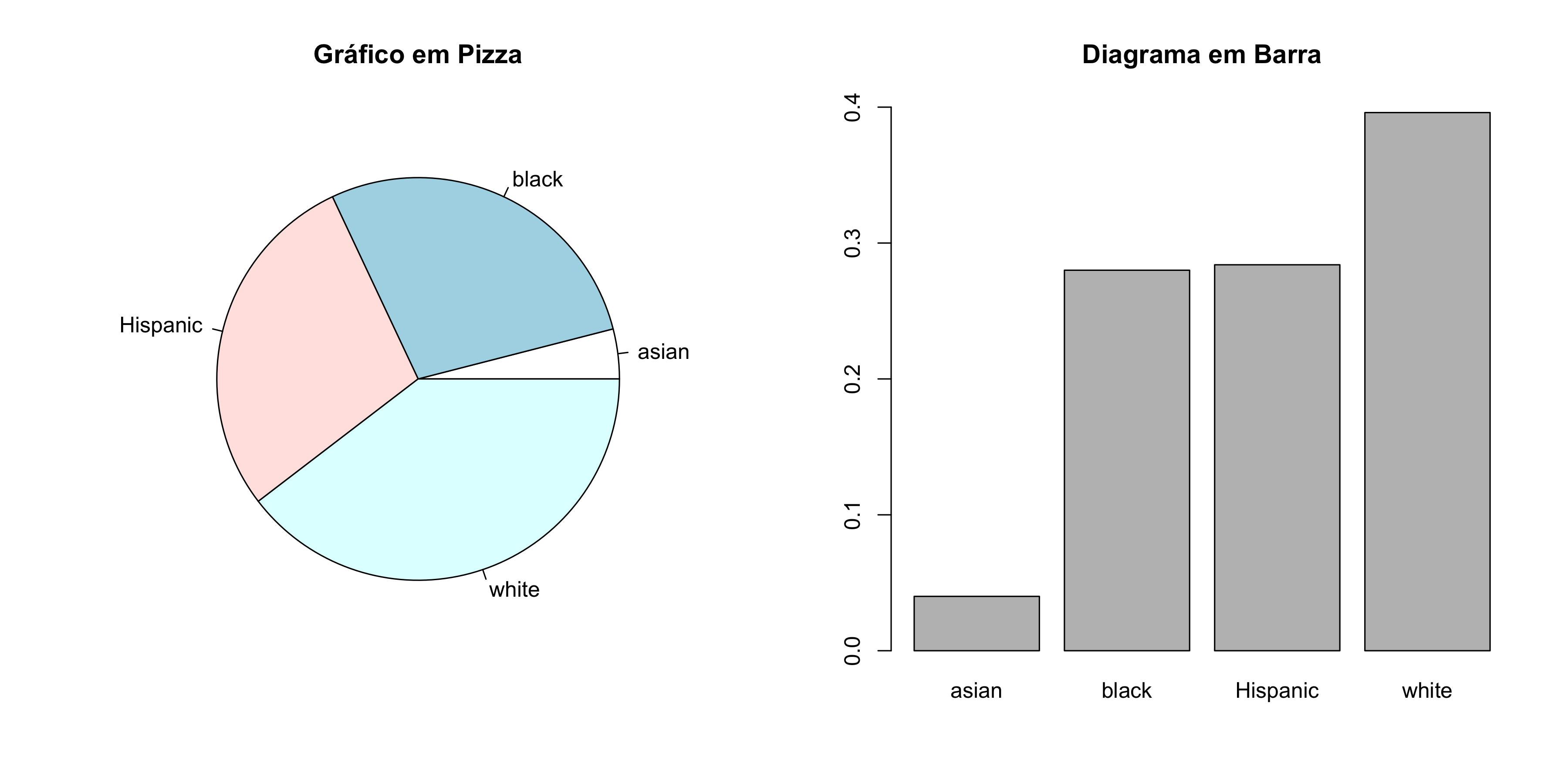
Variáveis qualitativas podem ser demonstradas graficamente. Os gráficos de barras ou em pizza são os mais utilizados (Figura 1).
Figura 1. Exemplos de gráficos para representação da proporção de amostras em cada classe de uma variável qualitativa.

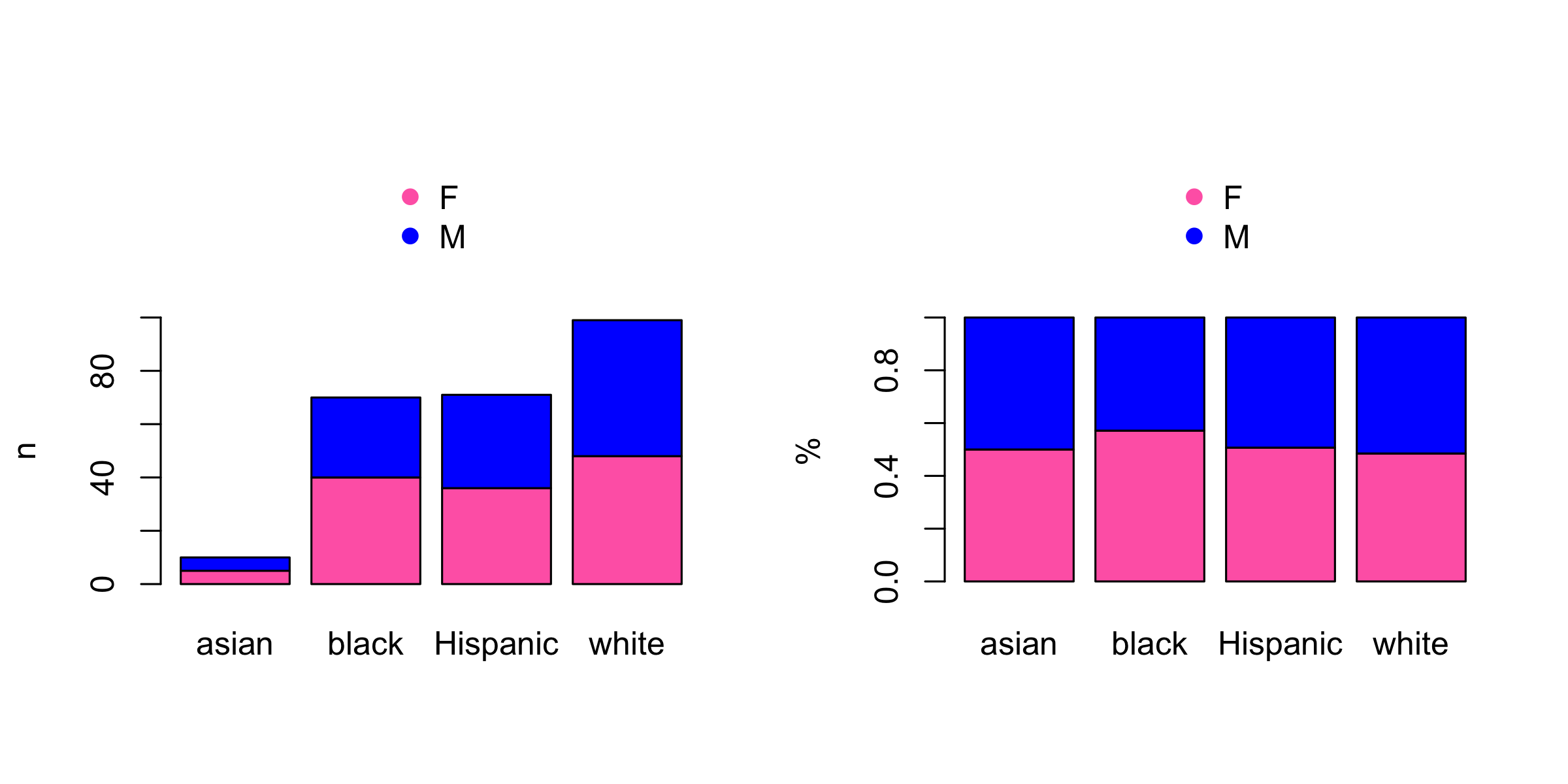
Podemos representar a distribuição entre duas variáveis qualitativas com um diagrama de barra. O diagrama pode mostrar a contagem de cada variável ou a proporção (Figura 2).
Figura 2. Distribuição de raça em relação com o gênero.
Podemos usar o script em R abaixo para gerar as medidas de tendência central e dispersão para cada variável quantitativa. A Tabela 2 resume a descrição da amostra.
# idade
summary(kid.weights$age)
sd(kid.weights$age)
IQR(kid.weights$age)
# peso
summary(kid.weights$weight)
sd(kid.weights$weight)
IQR(kid.weights$weight)
# altura
summary(kid.weights$height)
sd(kid.weights$height)
IQR(kid.weights$height)
#IMC
summary(kid.weights$bmi)
sd(kid.weights$bmi)
IQR(kid.weights$bmi)Tabela 2. Variáveis quantitativas.
| Variável | Média | \(\sigma\) | Mediana | Q1 | Q3 | AI |
|---|---|---|---|---|---|---|
Idade (meses) |
47.95 | 39.83 | 39.0 | 12.25 | 69.75 | 57.5 |
Peso (libra) |
38.38 | 24.8 | 32.0 | 22.0 | 45.0 | 23 |
Altura (polegada) |
36.52 | 10.7 | 36.0 | 28.0 | 43.0 | 15 |
IMC (kg/\(m^2\)) |
19.57 | 7.19 | 17.69 | 15.59 | 21.2 | 5.6 |
Em publicações científicas não utilizamos várias medidas de tendência central ou de dispersão. Temos que escolher uma. E como escolher a melhor medida para descrever o conjunto de dados? A recomendação é utilizar a média e o desvio padrão para variáveis com distribuição normal. Nesta situação, a média, mediana e a moda são sobrepostos e a medida do desvio padrão pode ser aplicada tanto para os valores acima ou abaixo da média, pois a curva de distribuição de frequências é simétrica (o testar para a normalidade será abordado em um próximo artigo).
Vejamos os gráficos na Figura 1 abaixo. O gráfico a esquerda representa a distribuição de frequência de idade em meses do banco de dados kid.weights. O gráfico não tem simetria e a média e mediana são diferentes. No gráfico a direita, os dados foram gerados aleatoriamente com a mesma média e desvio padrão e apresentam um distribuição normal. Veja a simetria da distribuição das frequências e a média e a mediana estão sobrepostas.
Figura 3. Distribuição de frequências de idade.
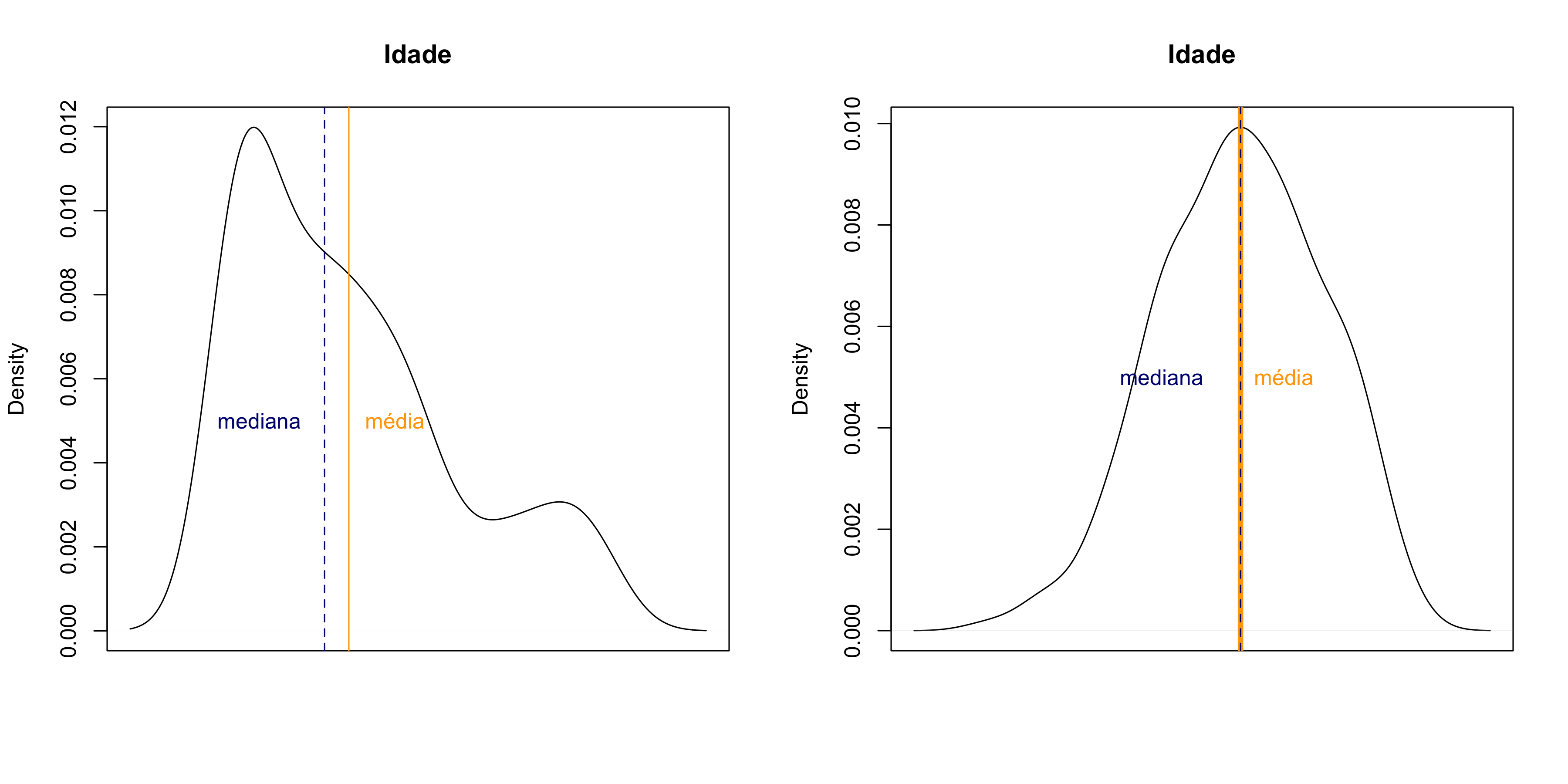
Nos casos onde a distribuição não é normal, a média não é uma boa representação da tendência central pela assimetria dos dados. O desvio padrão também não representa a dispersão de forma adequada, pois a distribuição de frequências não é simétrica. Neste caso, é mais adequado utilizar a mediana e a amplitude interquartil.
E como representar graficamente as variáveis quantitativas?
O boxplot ou diagrama de caixa é uma forma clássica de representação gráfica da de um conjunto de dados numéricos. Veja a figura abaixo e vamos entender a quantidade de informações que podemos ter com ela.
Figura 4. Boxplot da distribuição da idade.
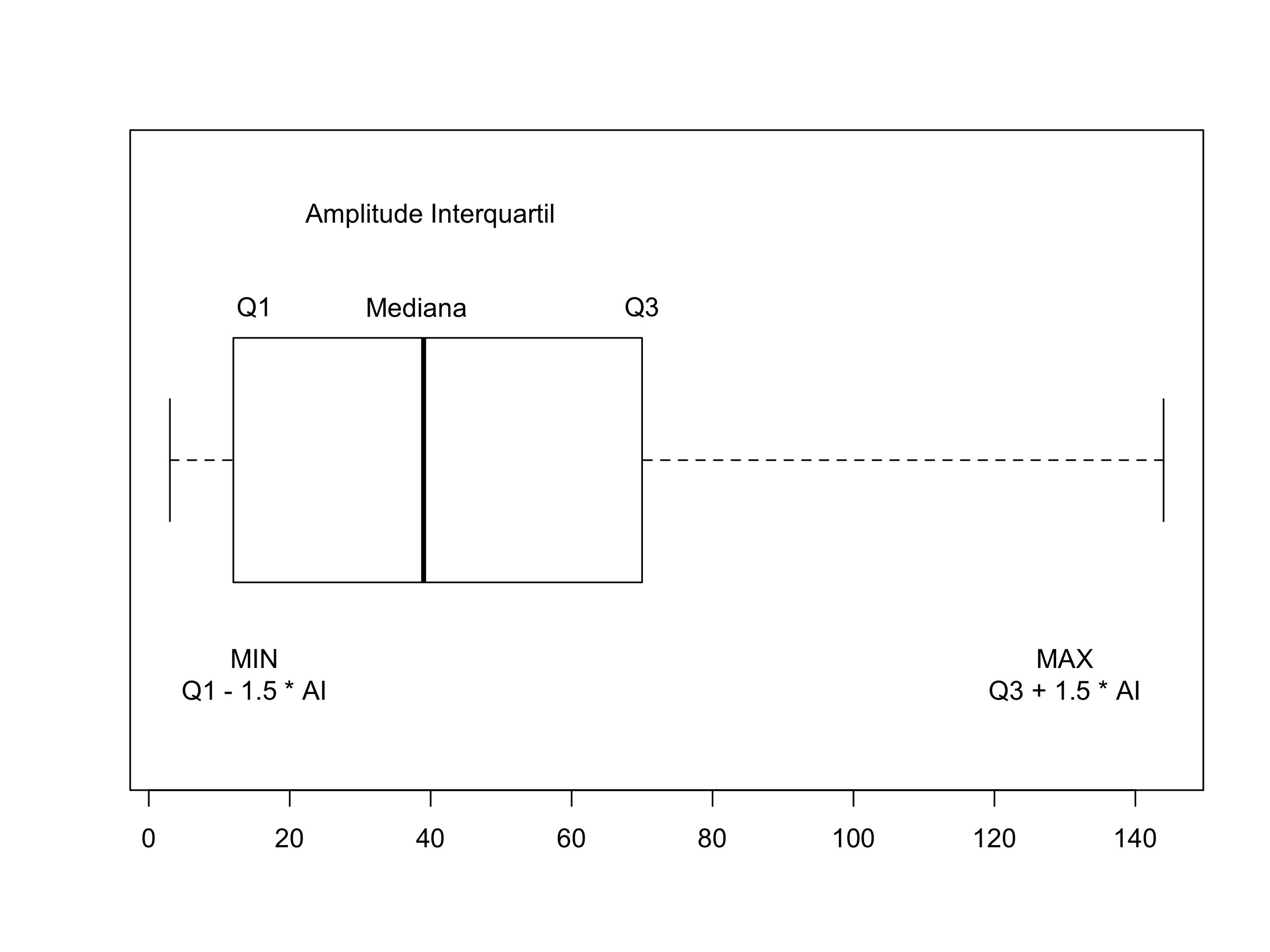
O boxplot mostra o valor da mediana, o Q1, o Q3, a amplitude interquartil e os valores mínimos e máximos que são baseados na subtração e adição de 1.5 vezes a AI do Q1 e Q3, respectivamente. Esses valores são os valores mínimos e máximos excluindo o que chamamos de outliers, que são valores muito discrepantes dos outros. Adicionalmente, podemos ter um inferência visual sobre a normalidade da distribuição. Note que a mediana e a caixa estão deslocados para a esquerda (note a semelhança com a distribuição de frequências na figura 3 à esquerda). Este é um sinal de que a distribuição parece não ser normal.
Podemos utilizar o boxplot para comparar a distribuição de valores quantitativos entre dois grupos. Veja na Figura 5 a comparação da altura entre crianças do sexo masculino e feminino.
Figura 5. Altura de crianças do sexo masculino (M) e feminino (F).
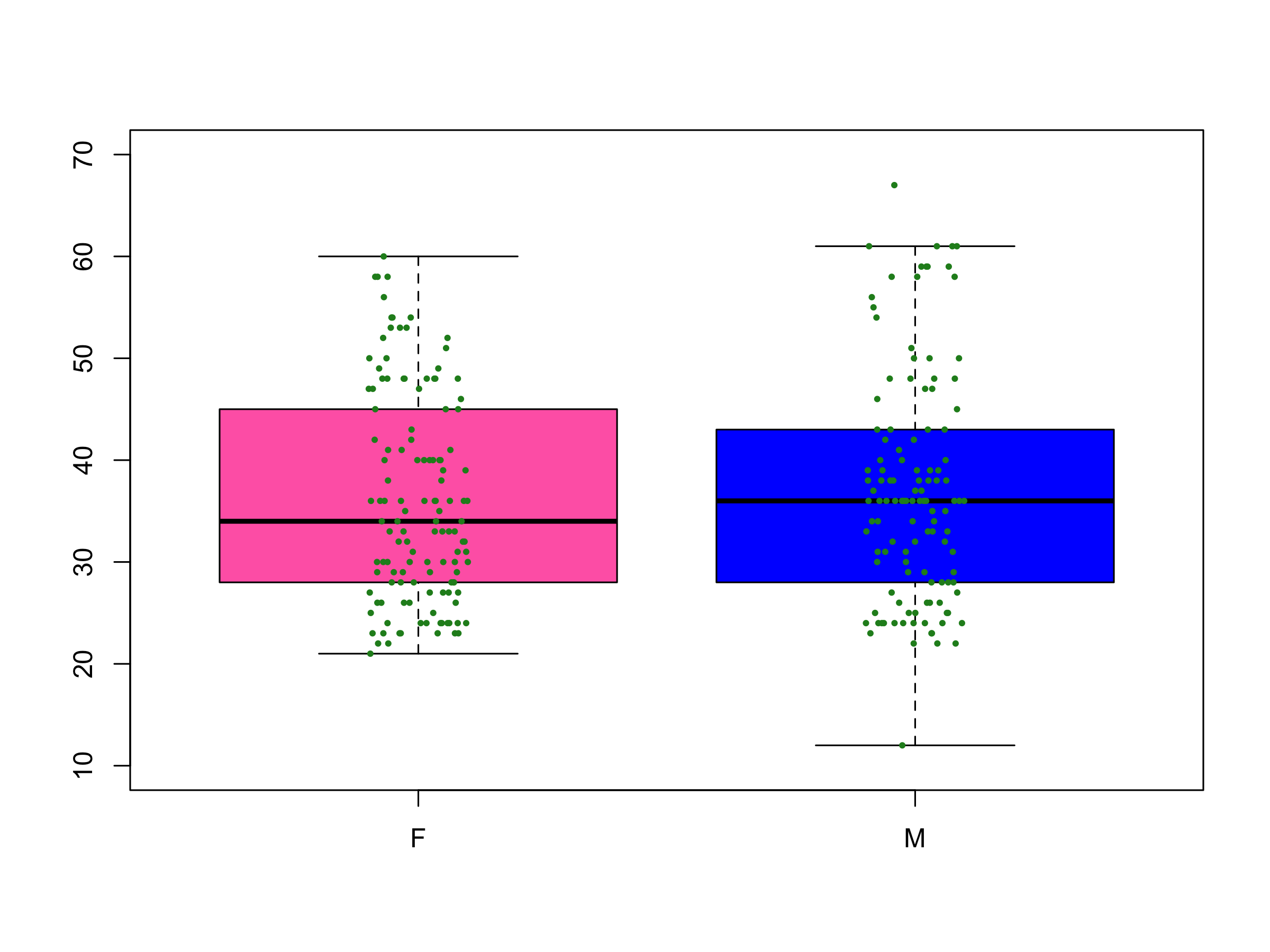
Com este gráfico podemos notar que a mediana da altura entre as crianças do sexo masculino (M) é um pouco maior que do feminino (F). A amplitude interquartil é menor em M. No entanto, as duas caixas são bem sobrepostas, o que sugere que não existir uma grande diferença entre os grupos. Note que existe um outlier na distribuição das alturas para o sexo masculino.
E quanto temos duas variáveis contínuas? Neste caso, podemos fazer um gráfico de uma em função da outra. Este gráfico é chamado de scatterplot ou gráfico de dispersão. Com este gráfico podemos fazer inferência sobre a correlação entre duas variáveis. Por exemplo, vamos analisar a Figura 6.
Figura 6. Peso em função da altura.
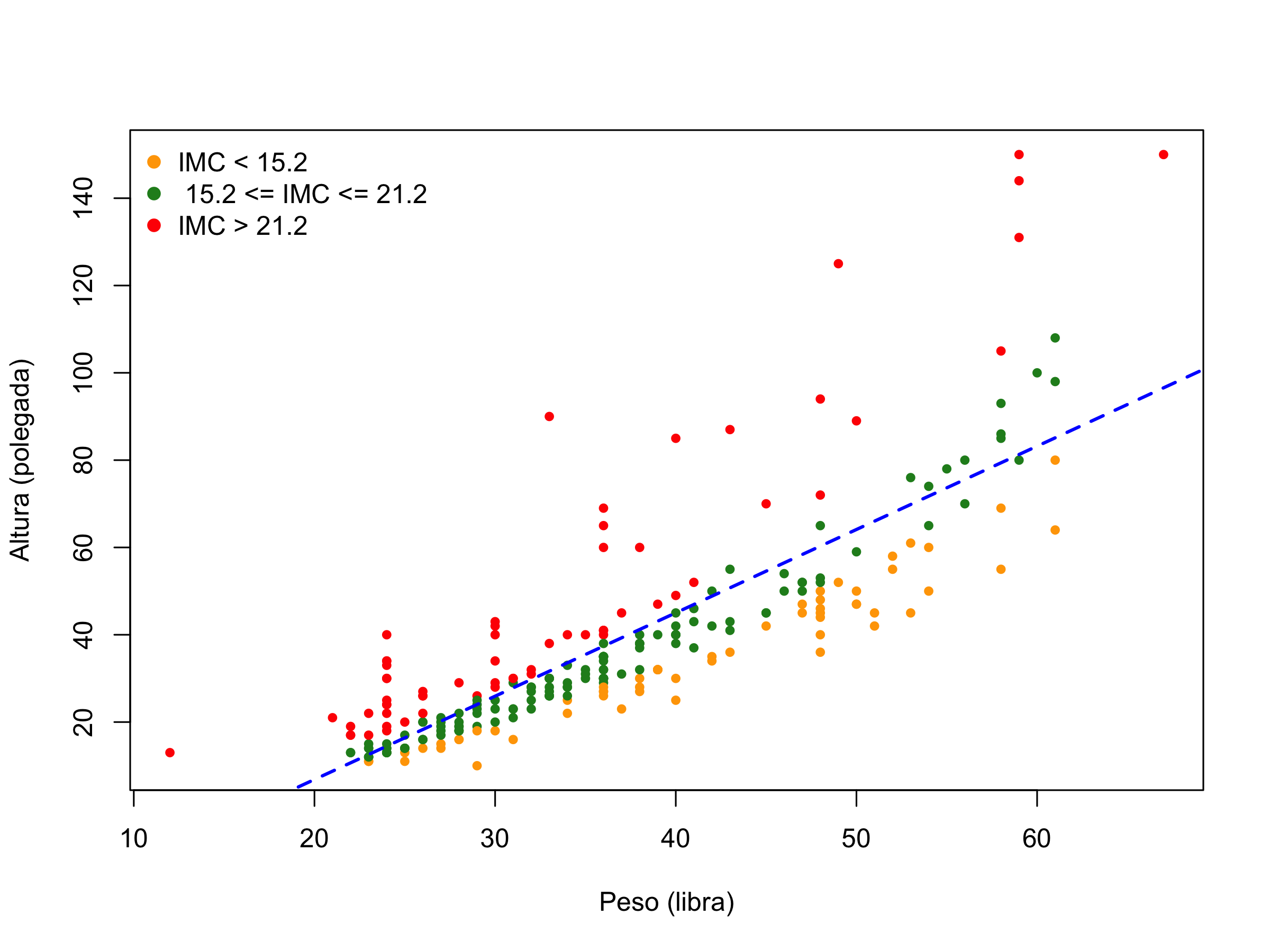
O gráfico mostra o peso em função da altura. A linha azul é a projeção da regressão linear. A inclinação da reta azul reflete o índice de correlação entre as duas variáveis (iremos ver esses conceitos nos próximos artigos). Note a linha azul sobrepõe os valores em verde, que são as crianças onde o IMC estão entre o Q1 e Q3. Crianças com IMC acima do Q1 são representados em vermelho, e os abaixo de Q1 na cor laranja.
## Códigos em R para implementação dos gráficos
# Figura 1
png("fig1.png", height = 6, width = 12, units = 'in', res = 300)
par(mfrow = c(1,2))
pie(table(kid.weights$race), main = 'Gráfico em Pizza')
barplot(prop.table(table(kid.weights$race)), ylim = c(0,.4), main = 'Diagrama em Barra')
dev.off()
# Figura 2
png("fig2.png", height = 4, width = 8, units = 'in', res = 300)
par(mfrow = c(1,2))
par(oma = c(0,0,4,0), xpd = T)
barplot(table(kid.weights$gender, kid.weights$race), ylim = c(0,100), ylab = "n", col = c("hotpink", "blue"))
legend('top', c('F', 'M'), inset = c(0.1,-0.6), pch = 19, col = c("hotpink", "blue"), bty = 'n')
barplot(prop.table(table(kid.weights$gender, kid.weights$race), 2), ylab = "%",col = c("hotpink", "blue"))
legend('top', c('F', 'M'), inset = c(0.1,-0.6), pch = 19, col = c("hotpink", "blue"), bty = 'n')
dev.off()
# Figura 3
ages <- rnorm(250, 47.95, 39.83)
png("fig3.png", height = 6, width = 12, units = 'in', res = 300)
par(mfrow = c(1,2))
plot(density(kid.weights$age), main = "Idade", xaxt='n', xlab = '')
abline(v=mean(kid.weights$age), col = 'orange')
abline(v=median(kid.weights$age), col = 'navy', lty = 2)
text(65,0.005,'média', col = 'orange')
text(15,0.005,'mediana', col = 'navy')
plot(density(ages), main = "Idade", xaxt='n', xlab = '')
abline(v=mean(ages), col = 'orange', lwd = 4)
abline(v=median(ages), col = 'navy', lty = 2)
text(70,0.005,'média', col = 'orange')
text(15,0.005,'mediana', col = 'navy')
dev.off()
# Figura 4
png("fig4.png", height = 6, width = 8, units = 'in', res = 300)
boxplot(kid.weights$age, horizontal = TRUE)
text(15, 1.25, 'Q1')
text(38, 1.25, 'Mediana')
text(70, 1.25, 'Q3')
text(40, 1.4, 'Amplitude Interquartil')
text(15, 0.65, 'MIN\nQ1 - 1.5 * AI')
text(130, 0.65, 'MAX\nQ3 + 1.5 * AI')
dev.off()
# Figura 5
png("fig5.png", height = 6, width = 8, units = 'in', res = 300)
boxplot(kid.weights$height ~ kid.weights$gender, outline = FALSE, col = c("hotpink", "blue"), ylim = c(10,70))
stripchart(kid.weights$height ~ kid.weights$gender, add = TRUE, method = 'jitter', vertical = T, pch=19,col = 'forestgreen', cex = .4)
dev.off()
# Figura 6
png("fig6.png", height = 6, width = 8, units = 'in', res = 300)
plot(kid.weights$height, kid.weights$weight, pch = 19, col=kid.weights$imc_colour, cex=.65,ylab = 'Altura (polegada)', xlab = 'Peso (libra)')
legend('topleft', legend = c("IMC < 15.2", " 15.2 <= IMC <= 21.2", "IMC > 21.2"), col = c("orange", " forestgreen", "red"), pch = 19, bty ='n')
abline(lm(kid.weights$weight ~ kid.weights$height), lty = 2, col = 'blue', lwd = 2)
dev.off()